群组重要性#
在本 Notebook 中,我们将展示如何计算和解释 InterpretML 全局解释中显示的 EBM 总体重要性。我们还将展示如何计算一组特征或项的重要性。
在本 Notebook 中,我们使用 term 来表示单个特征和交互项(成对)。
本 Notebook 可以在我们的 GitHub 示例文件夹中找到。
# install interpret if not already installed
try:
import interpret
except ModuleNotFoundError:
!pip install --quiet interpret pandas scikit-learn
训练用于回归任务的可解释增强机器 (EBM)
让我们使用 Boston 数据集作为参考并训练一个 EBM。
import numpy as np
import pandas as pd
from sklearn.datasets import load_diabetes
from interpret.glassbox import ExplainableBoostingRegressor
from interpret import set_visualize_provider
from interpret.provider import InlineProvider
set_visualize_provider(InlineProvider())
X, y = load_diabetes(return_X_y=True, as_frame=True)
ebm = ExplainableBoostingRegressor()
ebm.fit(X, y)
ExplainableBoostingRegressor()在 Jupyter 环境中,请重新运行此单元格以显示 HTML 表示或信任此 Notebook。
在 GitHub 上,HTML 表示无法渲染,请尝试使用 nbviewer.org 加载此页面。
ExplainableBoostingRegressor()
解释模型
EBM 提供两种不同的解释:关于整体模型行为的全局解释和关于模型个体预测的局部解释。
全局解释
全局解释有助于理解模型认为重要的地方,以及识别其决策或训练数据中的潜在缺陷。让我们首先计算并显示一个全局解释。
from interpret import show
show(ebm.explain_global(name='EBM'))
每个项的总体重要性计算为 该项(特征或对)在对整个训练数据集进行预测时所做的平均绝对贡献(得分)。 这种衡量项重要性的方式倾向于那些平均而言对许多案例的预测有很大影响的项。总体重要性不是正/负的衡量标准,而是衡量每个项在得分中的重要程度。对于回归,这些得分的单位与特征图的 y 轴单位相同。对于分类,得分将以 logit 为单位表示。
除了总体项重要性之外,由于 EBM 是可加模型,我们可以精确衡量每个项对预测的贡献。让我们通过在下拉菜单中选择项 bp 来查看其图。
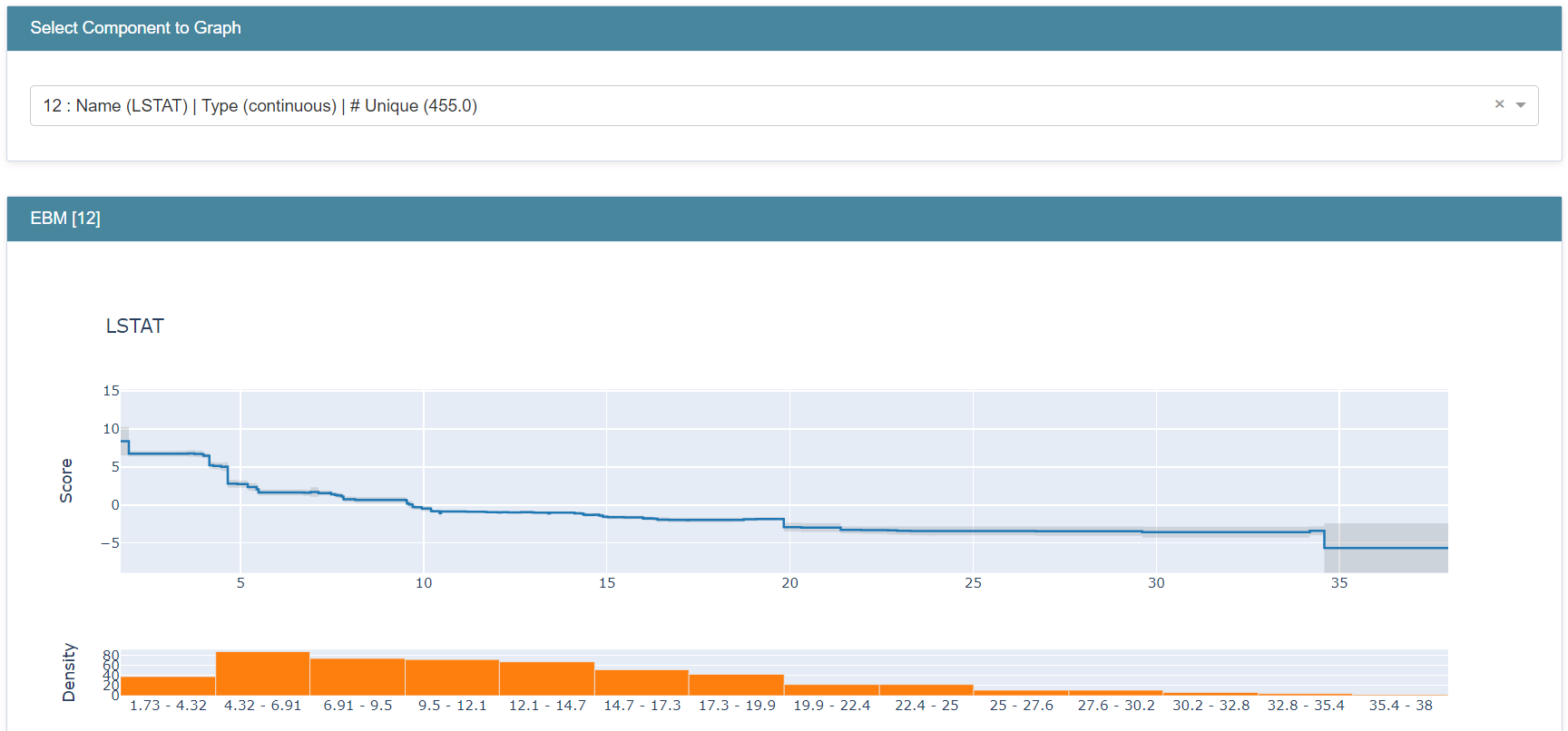
解释这一点的方式是,如果一个新的数据点 bp = 0.1,模型会在最终预测中增加约 +33.1。然而,对于 bp = 0.13 的不同数据点,模型现在会向预测增加约 +36.7。
为了进行个体预测,模型将每个项图用作查找表,记录每个项的贡献,并将它们与学习到的截距相加以得出预测。在回归中,截距是训练集的平均目标(标签),每个项会加到或减去此平均值。在分类中,截距反映了正类别在对数尺度上的基础概率。图上方和下方的灰色区域表示模型在该区域图中的置信度。
局部解释
通过局部解释,我们可以看到单个样本预测的完整细分。以下是计算数据集中第一个样本预测细分的方法:
from interpret import show
show(ebm.explain_local(X[:1], y[:1]), 0)
让我们通过在下拉菜单中选择来查看预测。
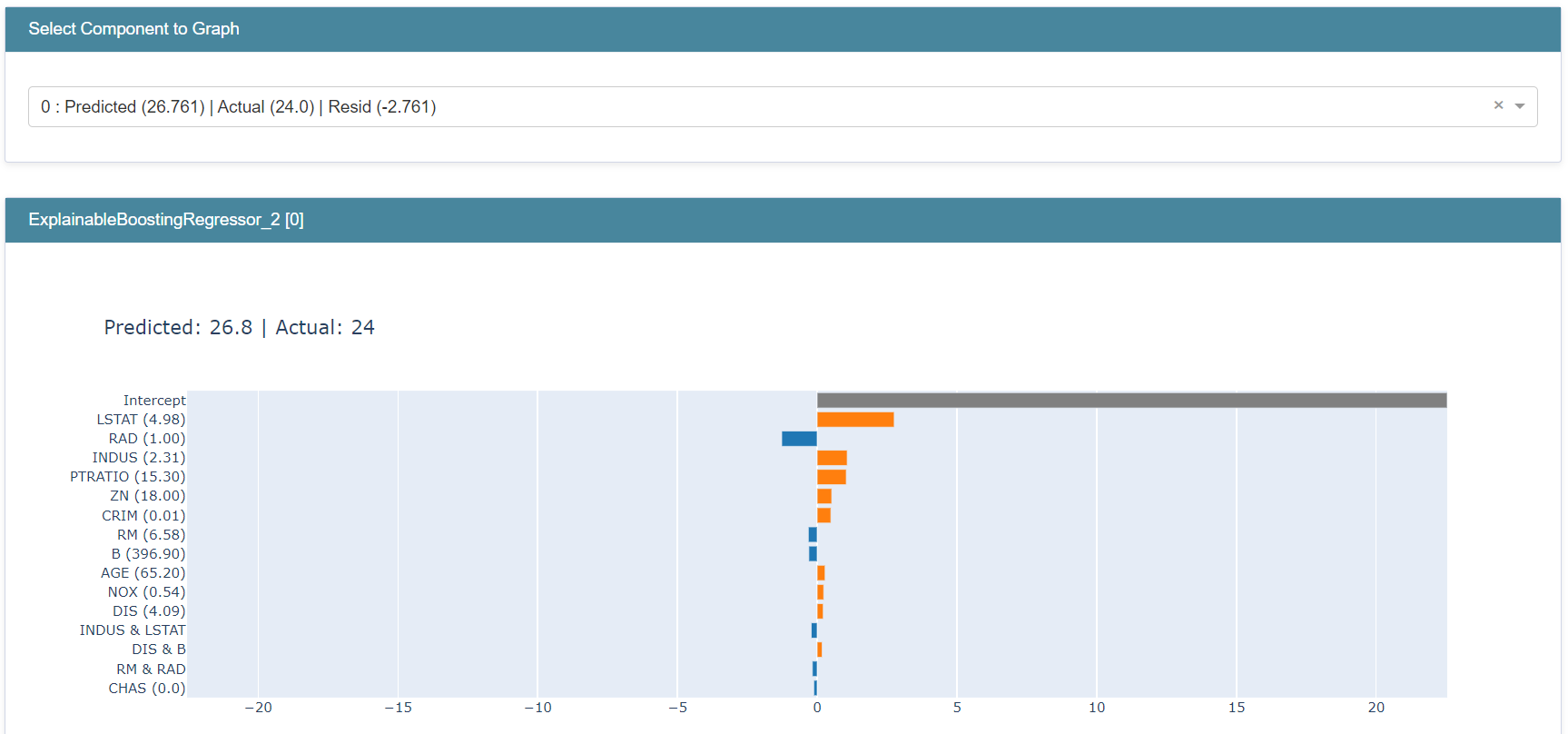
模型预测为 188.50。我们可以看到截距增加了约 +151.9,bp 减去了约 0.02,而 age 增加了约 0.04。如果我们对所有项重复此过程,我们将正好得到模型预测值 188.50。
查看 _所有_ 项重要性
由于图表空间限制,项重要性摘要仅显示前 15 个项。要查看训练好的 EBM 的所有项的总体重要性(即全局解释摘要中显示的得分),我们使用 term_importances()。
importances = ebm.term_importances()
names = ebm.term_names_
for (term_name, importance) in zip(names, importances):
print(f"Term {term_name} importance: {importance}")
Term age importance: 3.2357671259109337
Term sex importance: 10.431907227185329
Term bmi importance: 17.34189713649959
Term bp importance: 11.393360813850238
Term s1 importance: 1.535831437239701
Term s2 importance: 3.172597989399135
Term s3 importance: 7.2821022176597054
Term s4 importance: 6.054837490610567
Term s5 importance: 17.198646537608173
Term s6 importance: 5.152081623321795
Term age & bp importance: 0.5536396223751048
Term age & s5 importance: 0.6984218945466711
Term bmi & bp importance: 0.5590693940335197
Term bmi & s4 importance: 0.6422460778583943
Term bmi & s5 importance: 0.6387171855892041
Term bmi & s6 importance: 0.5569204313150303
Term bp & s1 importance: 0.41429582648349744
Term s1 & s5 importance: 0.6854762194624874
Term s5 & s6 importance: 0.8994164799584223
请注意,平均绝对贡献不是计算项重要性的唯一方法。我们的包提供的另一个指标是 min_max 选项,它计算每个项的 max(图上的最高分)和 min(图上的最低分)值之间的差。使用 min_max 衡量的重要性是衡量项可能产生的最大影响,即使这种影响可能只发生在极少数情况下;而 avg_weight(默认参数)衡量的是项在所有案例中的典型(平均)贡献。
importances = ebm.term_importances("min_max")
names = ebm.term_names_
for (term, importance) in zip(names, importances):
print(f"Term {term} importance: {importance}")
Term age importance: 16.3031783304845
Term sex importance: 20.947878749427844
Term bmi importance: 99.88236502169572
Term bp importance: 70.5812655361787
Term s1 importance: 13.631773120507084
Term s2 importance: 19.631457279237022
Term s3 importance: 53.12806663213374
Term s4 importance: 28.821515052870232
Term s5 importance: 63.81503875799717
Term s6 importance: 36.767153432203166
Term age & bp importance: 5.711542514690193
Term age & s5 importance: 7.361992350063598
Term bmi & bp importance: 10.058669470849502
Term bmi & s4 importance: 4.093351889650322
Term bmi & s5 importance: 6.154372852444338
Term bmi & s6 importance: 5.333647095242265
Term bp & s1 importance: 6.524589504610913
Term s1 & s5 importance: 8.681891134556814
Term s5 & s6 importance: 10.999279605767754
特征/项群组重要性
我们提供了实用函数来计算特征或项组的重要性,并且可以选择将这些重要性附加到全局特征归因条形图。请注意,不对特征/项组生成形状函数图,仅在摘要中显示其总体重要性。
将项分组然后计算并显示其重要性不会以任何方式改变模型及其做出的预测——群组重要性只是一种计算项组重要性的方法,是对已计算的单个项重要性的补充。正如您在下面的示例中看到的,特征/项在不同组中重叠是可以的。
计算群组重要性
让我们使用 Adult 数据集并训练用于分类任务的 EBM。
import numpy as np
import pandas as pd
from interpret.glassbox import ExplainableBoostingClassifier
df = pd.read_csv(
"https://archive.ics.uci.edu/ml/machine-learning-databases/adult/adult.data",
header=None)
df.columns = [
"Age", "WorkClass", "fnlwgt", "Education", "EducationNum",
"MaritalStatus", "Occupation", "Relationship", "Race", "Gender",
"CapitalGain", "CapitalLoss", "HoursPerWeek", "NativeCountry", "Income"
]
X = df.iloc[:, :-1]
y = df.iloc[:, -1]
adult_ebm = ExplainableBoostingClassifier()
adult_ebm.fit(X, y)
ExplainableBoostingClassifier()在 Jupyter 环境中,请重新运行此单元格以显示 HTML 表示或信任此 Notebook。
在 GitHub 上,HTML 表示无法渲染,请尝试使用 nbviewer.org 加载此页面。
ExplainableBoostingClassifier()
然后我们创建一个由项组成的列表——单个特征或交互项——作为我们的群组并计算其重要性。
from interpret.glassbox._ebm._research import *
social_feature_group = ["MaritalStatus", "Relationship", "Race", "Gender", "NativeCountry"]
importance = compute_group_importance(social_feature_group, adult_ebm, X)
print(f"Group: {social_feature_group} - Importance: {importance}")
Group: ['MaritalStatus', 'Relationship', 'Race', 'Gender', 'NativeCountry'] - Importance: 1.34025432582611
在这个例子中,我们创建一个包含五个项的群组并计算其重要性。与单个特征重要性类似,我们将此分数解释为 该项组在对整个训练数据集进行预测时所做的平均绝对贡献。 请注意,对于每个预测,组中每个项的贡献将被相加,然后再取绝对值。
我们还可以选择创建包含群组重要性的全局解释,或将其附加到现有解释中。
my_global_exp = append_group_importance(social_feature_group, adult_ebm, X)
show(my_global_exp)
social_feature_group 的重要性约为 1.30,这高于任何单个特征/项的重要性。
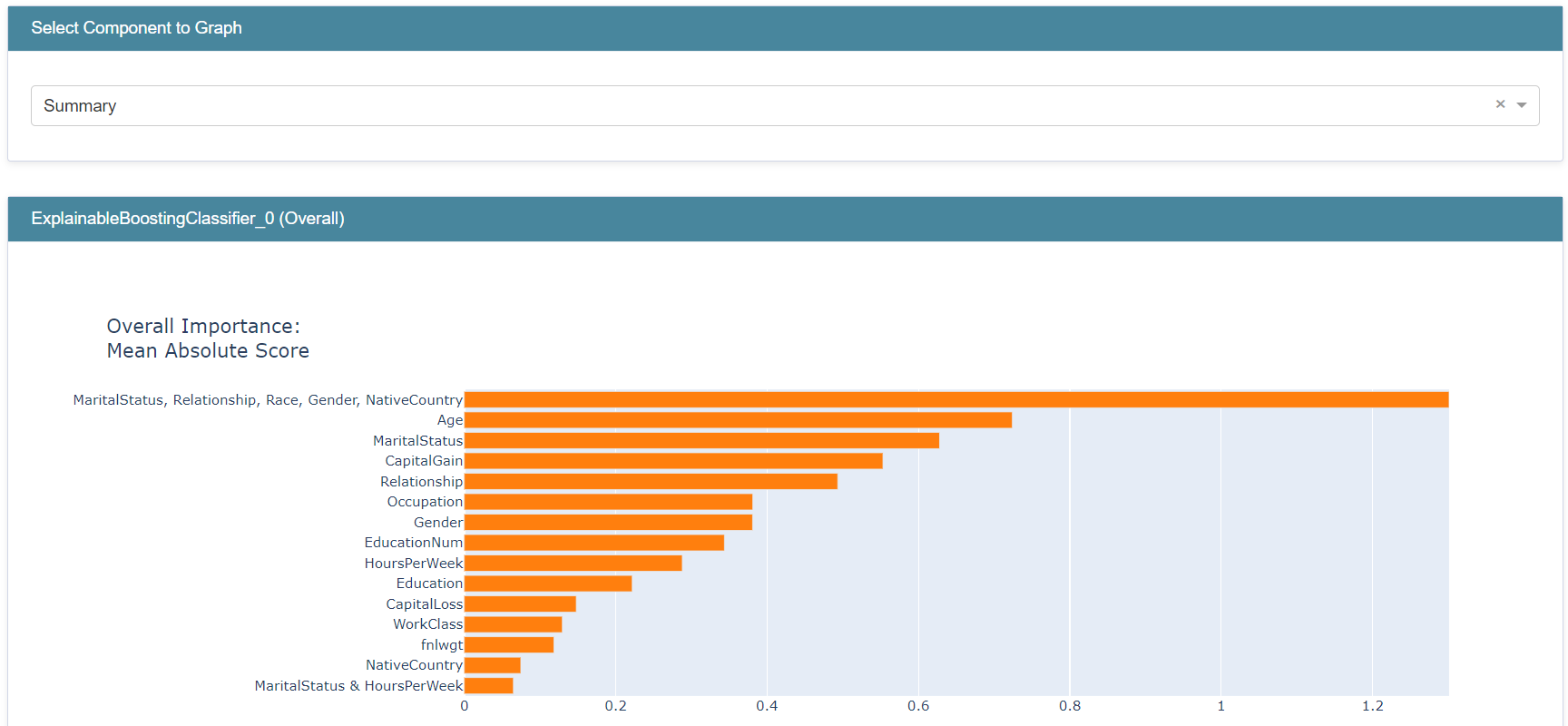
我们也可以在不同群组之间进行这种类型的比较。
education_feature_group = ["Education", "EducationNum"]
relationship_feature_group = ["MaritalStatus", "Relationship"]
social_feature_group = ["MaritalStatus", "Relationship", "Race", "Gender", "NativeCountry"]
my_global_exp = append_group_importance(social_feature_group, adult_ebm, X)
my_global_exp = append_group_importance(education_feature_group, adult_ebm, X, global_exp=my_global_exp)
my_global_exp = append_group_importance(relationship_feature_group, adult_ebm, X, global_exp=my_global_exp)
show(my_global_exp)
education_feature_group 的重要性约为 0.52,高于其各自的单个项,但小于某些单个项,例如 Age。记住,创建特征/项组不会以任何方式改变模型及其预测,它只允许您估计这些组的重要性。
例如,此图表明与关系相关的特征比与教育相关的特征更重要。
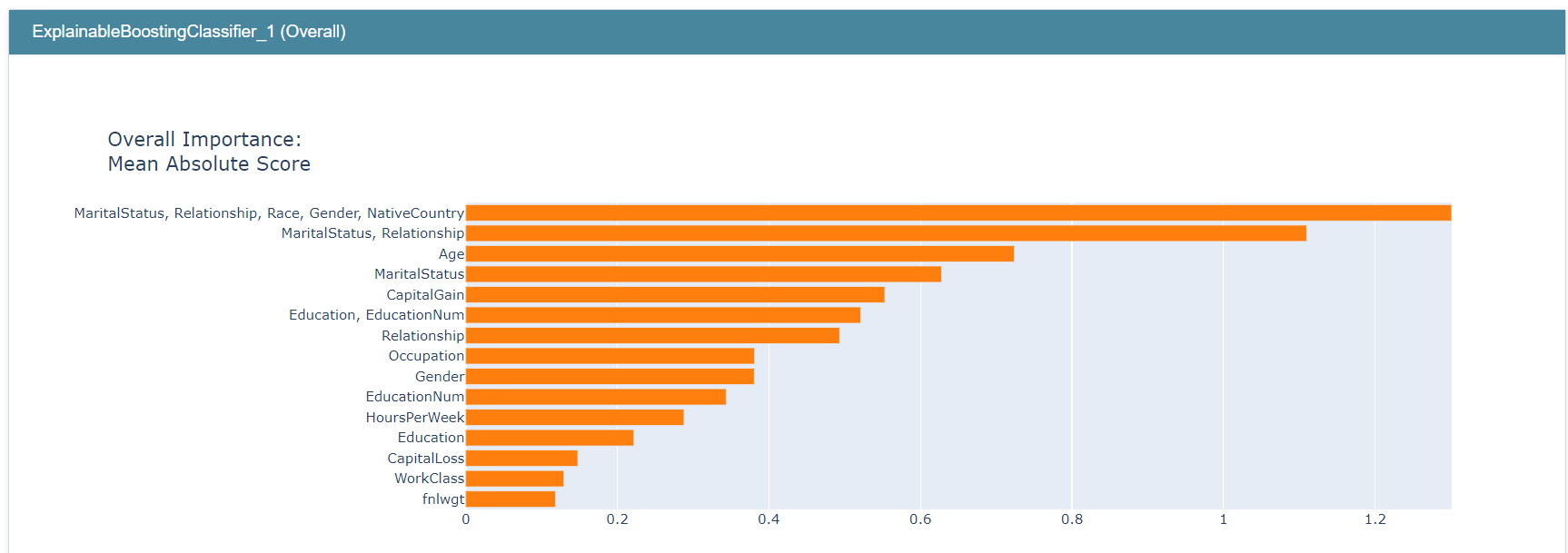
我们还可以将我们感兴趣的一个群组(例如 social_feature_group)与所有其他剩余项组成的群组进行比较。
social_feature_group = ["MaritalStatus", "Relationship", "Race", "Gender", "NativeCountry"]
all_other_terms = [term for term in adult_ebm.term_names_ if term not in social_feature_group]
my_global_exp = append_group_importance(social_feature_group, adult_ebm, X)
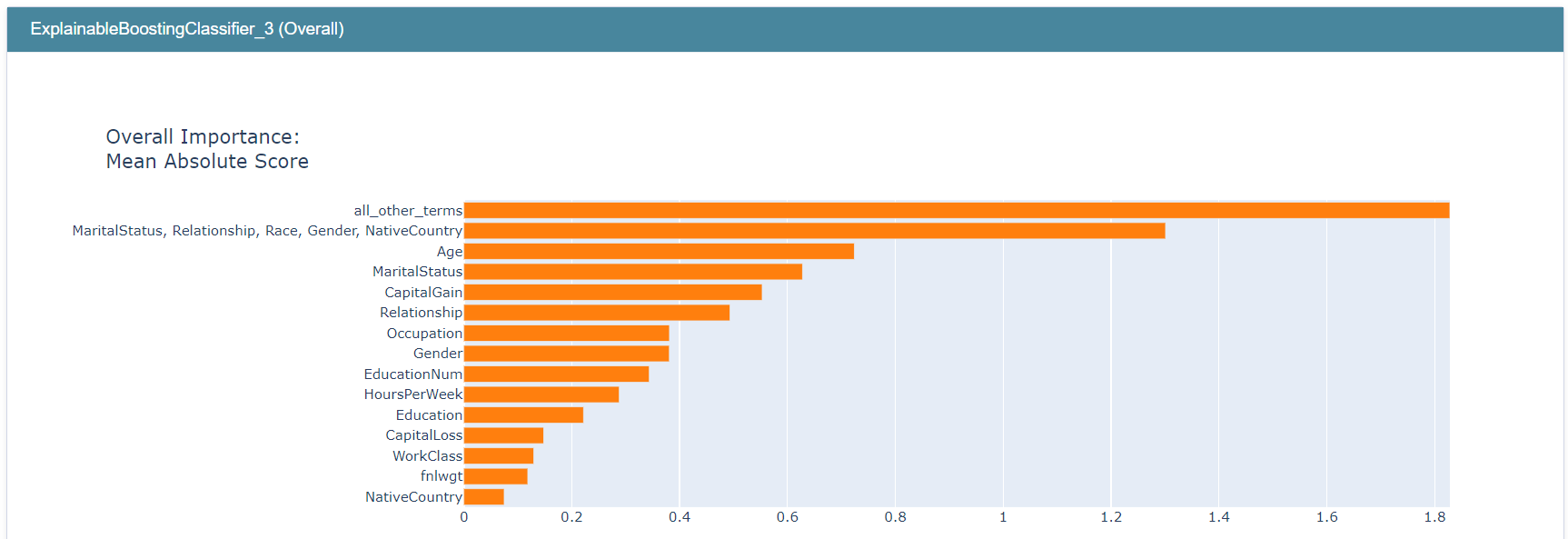
my_global_exp = append_group_importance(all_other_terms, adult_ebm, X, group_name="all_other_terms", global_exp=my_global_exp)
show(my_global_exp)
请注意,all_other_terms 具有最高的重要性得分,其次是 social_feature_group。
甚至可以创建一个包含所有项的群组。
all_terms_group = [term for term in adult_ebm.term_names_]
mew_global_exp = append_group_importance(all_terms_group, adult_ebm, X, group_name="all_terms")
show(mew_global_exp)
最后,我们还提供了一个函数来计算一组项以及模型所有原始项的重要性。
my_dict = get_group_and_individual_importances([social_feature_group, education_feature_group], adult_ebm, X)
for key in my_dict:
print(f"Term: {key} - Importance: {my_dict[key]}")
Term: MaritalStatus, Relationship, Race, Gender, NativeCountry - Importance: 1.34025432582611
Term: MaritalStatus - Importance: 0.9601033154733993
Term: Age - Importance: 0.9075504363031826
Term: CapitalGain - Importance: 0.7242090336171584
Term: Education, EducationNum - Importance: 0.513598199392493
Term: Occupation - Importance: 0.42065530988090966
Term: Gender - Importance: 0.39234898577594574
Term: Education - Importance: 0.3657090790264731
Term: HoursPerWeek - Importance: 0.295931834424345
Term: Relationship - Importance: 0.2697701281793175
Term: CapitalLoss - Importance: 0.17264993670426207
Term: EducationNum - Importance: 0.16219654512179993
Term: fnlwgt - Importance: 0.12630437546911447
Term: WorkClass - Importance: 0.11054790459401066
Term: NativeCountry - Importance: 0.10590814015759697
Term: Age & HoursPerWeek - Importance: 0.08705249809717623
Term: MaritalStatus & HoursPerWeek - Importance: 0.07200169386624186
Term: Race - Importance: 0.06401839354691273
Term: Age & Education - Importance: 0.05583959640954401
Term: Age & fnlwgt - Importance: 0.04083269718186386
Term: EducationNum & MaritalStatus - Importance: 0.03924505860470226
Term: Age & Occupation - Importance: 0.033552252065613485
Term: Relationship & HoursPerWeek - Importance: 0.027857079254725758
Term: fnlwgt & Education - Importance: 0.027766538995828705
Term: Age & EducationNum - Importance: 0.024768728763885493
Term: Age & Race - Importance: 0.020665493626763193
Term: Age & Relationship - Importance: 0.016400416447842223
Term: WorkClass & Relationship - Importance: 0.014481754580273691
Term: WorkClass & Race - Importance: 0.006825066959667514
